| A | B |
|---|
| What is the associative property of addition? | States that you can group complex numbers in a sum in any way you want and still get the same answer (for example: (5-3)+(2+6)+(1-2) = (7+3)+(1-2) = (5-3)+(3+4) = 9 |
| What is the distributive property of addition? | Used when you multiply a complex number by the sum of two other numbers. The results will be the same whether you multiply first, then add, or add first, then multiply (for example: 3(2+4) = 3*2 +3*4 = 18 OR = 3*6 = 18 |
| What's another word for natural numbers and what are natural numbers? | Counting numbers = {1,2,3,...} |
| What's another word for counting numbers and what are counting numbers? | Natural numbers = {1,2,3,...} |
| What are whole numbers? | Whole numbers = {0,1,2,3, ...} |
| What are integers? | Integers = {... -3, -2, -1, 0, 1, 2, 3, ...} |
| What are rational numbers? | Rational numbers ={P/Q where P and Q are integers and Q doesn't = 0} |
| What are irrational numbers? | Irrational numbers = {nonterminating, nonrepeating decimals} = numbers that cannot be written in the form of P/Q where Q doesn't equal zero} |
| What are real numbers? | Real numbers = all rational numbers and all irrational numbers. Natural numbers, whole numbers, integers, rational and irrational numbers are subsets of real numbers. Every point on a number line corresponds to a real number. |
| What is the commutative property of addition? | The commutative property tells you that you can add 2 numbers in any order you want and still get the same answer. |
| What does the "Existence of an Additive Inverse" tell you? | For every complex number, there exists a partner that will add to that complex number to give zero as a sum. |
| What are the general forms of the sin and cosine functions? | y=a(sin OR cos)(bx-c)+k. The graph will have an amplitude = a, period=2pie/b, horizontal shift = c/b (to the right of origin if positive and to the left if negative), vertical shift = k (up from origin if positive and down if negative) |
| Sin of zero = ____ | 0 |
| Cos of zero = ____ | 1 |
| What are complex numbers? | complex #'s = x + yi (where x and y are real numbers and i^2 = -1 (When x = zero, the resulting set is pure imaginary numbers. When y = zero, the resulting set consists of real numbers) |
| What is pie = to in degrees? | 180,  |
| How do you plot points on a complex plane? | .,  |
| Which axis is the real axis and which axis is the imaginary axis in a complex plane? | X axis is the real axis and the y axis is the imaginary axis, 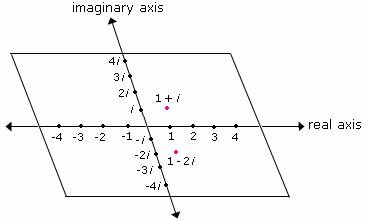 |
| How do you know if sets of ordered pairs represent a function? For example: {(2,3), (4,3), (8,3)} vs. {(4,5), (3,1), (3,10)} | A function is a relation in which each first component is paired with one and only one second component. Therefore, for the two sets of ordered pairs {(2,3), (4,3), (8,3)} vs. {(4,5), (3,1), (3,10)}, only the first set is a function. In the second set, the 3 is paired with both a 1 and a 10. |
| The domain of a function is all the possible ____ values while the range is all the possible ___ values. | x, y |
| All the possible x values of a function is called the ______ of the function | domain |
| All the possible y values of a function is called the ______ of the function | range |
| What is the technique of completing the square good for? | solving quadratic equations (see http://www.youtube.com/watch?v=xGOQYTo9AKY for an easy example and http://www.youtube.com/watch?v=zKV5ZqYIAMQ&feature=fvwp&NR=1 for a slightly harder example where the a in ax^2 + bx +c = 0 is not a 1 |
| What is the general form of the quadratic equation? | y= ax^2 + bx +c (remember to set y=0 if you want to find where the function crosses the x axis) |
| What is the law of sines and what is it good for? | Sin angle A / length of opposite side a = Sin angle B / length of opposite side b = Sin angle C / length of opposite side c (Good for solving a non-right triangle) |
| What is the law of cosines and what is it good for? | c^2 = a^2 + b^2 - 2ab(cos of Angle C) (Good for solving a non-right triangle. Just remember that the side is opposite of the angle of the same letter)) |
| What 3 numbers do you have to remember for standard deviations? | 68, 95, and 99.7 (On a bell curve, 68% of the values fall within 1 standard deviation of the mean, 95% fall within 2 standard deviations and 99.7 fall within 3 standard deviations of the mean.) |
| What is the quadratic formula for solving quadratic equations?? Which part is the descrimant, and what can the descriminant tell you? | x= -b plus or minus the square root of b^2-4ac all divided by 2a (the part inside the square root is called the descriminant. If b^2-4ac = 0, the graph crosses the x axis in one place, if it is > 0, then is crosses in two places, if it is < 0 it doesn't cross the x axis. When using the quadratic equation, set y = 0 for the general format y = ax^2 + bx + c) |
| What is a vertical asymptope? | The value of x where the curve goes straight up (ie - y = infinite because the denominator of the equation becomes zero) |
| What are prime numbers? | Numbers that are only divisible by themselves and nothing else. 1 is not a prime #) |
| What does the derivitive on an equation tell you? | Once you get the derivitive of an equation, you can solve for the slope that is tangent to the curve at a certain x value on the curve. For example, the equation y=2x^3 + x + 3 is f'(x)=6x^2 + 1, you can plug in any x value and find the tangent slope at the point on the original so if you want to know the tangent slope at a certain x value on the original equation, just plug in that x value to the derivitive equation. For example, at x=2, the slope of the line tangent to the curve would be m=25. You can find the exact coordinate where that line is tangent by plugging in 2 to the original equation f(2)=2x^3 + x + 3 which is equal to 21, so the coordinate is (2,21 where a line with a slope of 25 is tangent to that curve. |
| If you know a coordinate and the slope of a line, how can you express the equation of that line? | Use the slope intercept format. y - the y coordinate = m(x - the x coordinate). For instance, if you know the slope is 2 and one of the points on the line is (3,4), then y-4=2(x-3) which is y-4 = 2x-6, then rearrange to get variables on left side with x being positive. So y-2x= -2 so 2x-y=2 |
| When dealing with inequalities, such as -X<3, what do you have to do to make x positive? | Multiply both sides be -1 AND flip the sign. (Remember, any equation that has an inequality can be solved just like it had an equal sign, but if the x ends up being negative, multiply both sides by -1 and flip the inequality sign) |
| What is the definition and value of e? | e=circumference of a circle divided by it's diameter = which is is a constant that is equal to 2.72 (remember that the ln(e) =1 |
| What is the natural log (ln) of e? | ln(e) = 1 |
| How can you rewrite lnA^x? | xlnA |
| What is the natural log (ln) of 1? | zero |
| What does i equal? What does i^2 equal? | i = square root of -1. i squared = -1 |
| What's the repeating pattern for i^n | i^1=i, i^2=-1, i^3=-i, i^4=1, then it repeats itself starting with i^5= i (so if you are asked what i^n is equal to, divide n by 4 and then use what's left over as your n for i^n. |
| If you have ln(x)=y and you are given y, how do you solve for x? | x=e^y (Remember, if you took the natural log of both sides of this, you would have ln(x)=lne^y=ylne and since ln(e)=1, you would end up with ln(x)=y. |
| What is the compound interest formula? | P(final) = P(initial)X(1+r)^t (If you have to solve for r or t, you will need to use some natural log and e hocus pocus. Just remember that ln(x)=y can be converted to x=e^y and visa versa) |
| How do you find the vertical asymptote of an equation? | Set the denominator of the equation to zero and solve (see http://www.purplemath.com/modules/asymtote4.htm ) |
| How do you find the horizontal asymptote of an equation. | An equation has a horizontal asymptote if the degree of the highest degree of the denominator is equal to or greater than the highest degree of the numerator? If it is greater, the horizontal asymptote is = 0 (because the denominator will get bigger faster than the numerator and the y value will approach zero). If the highest degree of both the numerator and denominator are the same, divide the terms of the highest numerator by the terms of the highest denominator. For example, if y = (4x^3 +2x)/(x^3 + 3), then the horizontal asymptote can be found by setting y=4x^3/x^3 = 4. As the x values get bigger, the other terms in the original equation become insignificant and y approaches the horizontal asymptote of 4. ((see http://www.purplemath.com/modules/asymtote4.htm ) |
| How do you know when there is an oblique (aka "slant") asymptote and how do you find it? | There is an oblique asymptote when the highest degree of the numerator is exactly 1 greater than the highest degree of the denominator. To find it, use long division to divide the numerator by the denominator. The oblique asymptote can be found as the answer to that long division and you can disregard any remainders because they become insignificant as the curve approaches the asymptote (see http://www.youtube.com/watch?v=--vh9zgZZmQ ) |
| How do you write a^y=x as in log form? | log(<sub>a)x = y (a is the base of the log. The base to the y power = x. Remember, if there is no subscript written after log, it is assumed that the base is 10) |
| How do you write log(<sub>a)x = y without the log? | a^y=x (a is the base in a log function. Remember, if there is no subscript written after log, it is assumed that the base is 10) |
| How can the function logX=Y be rewritten without the log? | 10^y=X (Remember, if there is no subscript written after log, it is assumed that the base is 10) |
| How can you factor the following function? logX + log(2x+2) = Y | logx(2x+2)=y (the base is 10 in this case. So it can also be written as 10^y = x(2x+2) and then you can solve.) |