|
|
|
1.
|
In the figure shown, 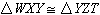 . .
Which statement is
NOT necessarily true? |  | | |
|
|
|
2.
|
With the information given in the drawings, which pair of triangles can be
proven congruent by the Angle-Side-Angle postulate?
|
|
|
3.
|
In the figure shown,
what is  ? ? | 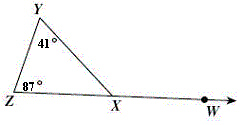 | | |
|
|
|
4.
|
Given: Segment AD congruent to segment
AC and
Angle DBA congruent to angle CEA
Which could be used to prove 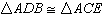 ? ? | 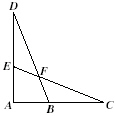 | | |
A) | (AAS) If 2 angles and the side between them in one triangle are congruent to 2
angles and the side between them in another triangle, then the triangles are
congruent | B) | (SAS) If 2 angles and a side not between them in one triangle are congruent to
2 angles and a side not between them in another triangle, then the triangles are
congruent | C) | (ASA) If 2 angles and the side between them in one triangle are congruent to 2
angles and the side between them in another triangle, then the triangles are
congruent | D) | (SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle,
then the triangles are congruent. |
|
|
|
5.
|
Use the proof to answer the question below: What reason can be used to
prove that the triangles are congruent?
|
|
|
6.
|
If  , which statement is always true?
|
|
|
7.
|
The figure has angle measures as shown.
What is the measure of 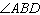 ? ? | 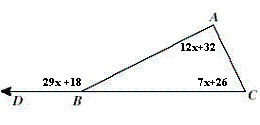 | | |
|
|
|
8.
|
Given: M is the midpoint of segments LN and
KP
The given
information is sufficient to prove 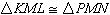 by which
postulate/theorem? by which
postulate/theorem? | 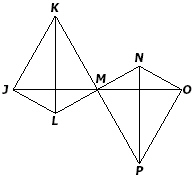 | | |
A) | Side-Angle-Side | C) | Angle-Angle-Side | B) | Angle-Side-Angle | D) | Side-Side-Side |
|
|
|
9.
|
Using the information given, which congruence postulate or theorem can be used to prove that 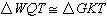 ? ? | 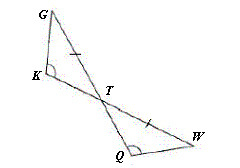 | | |
A) | Hypotenuse-Leg Theorem | C) | Side-Angle-Side Postulate | B) | Side-Side-Side
Postulate | D) | Angle-Angle-Side
Theorem |
|
|
|
10.
|
Which set of information
is
NOT enough to prove that  is congruent to is congruent to  ? ? | | | |
|
|
|
11.
|
Which of the following is the measure of the supplement of  ? ? | 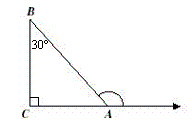 | | |
|
|
|
12.
|
Given: Segment AC congruent to segment
AB and
Angle CAD congruent to angle BAD
Which could be used to prove 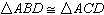 ? ? | 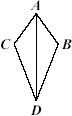 | | |
A) | (SAS) If 2 sides and the angle between them in one triangle are congruent to 2
sides and the angle between them in another triangle, then the triangles are
congruent | B) | (ASA) If 2 angles and the side between them in one triangle are congruent to 2
angles and the side between them in another triangle, then the triangles are
congruent | C) | (AAS) If 2 angles and a side not between them in one triangle are congruent to
2 angles and a side not between them in another triangle, then the triangles are
congruent | D) | (SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle,
then the triangles are congruent |
|
|
|
13.
|
Given: ABCD is a parallelogram. Prove: 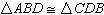 | 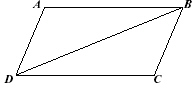 | Statements | Reasons | | Opposite angles of a parallelogram are congruent | | Opposite sides of a parallelogram are congruent | | Opposite sides of a parallelogram are congruent | | |
Therefore,  by which postulate/theorem?
|
|
|
14.
|
Given: E is a midpoint of AC
Angle DAE congruent to angle
BCE
Based on the information given, | 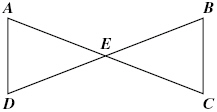 | | |
which triangle
congruence theorem could be used to prove  ? ?
A) | Side-Angle-Side (SAS) | C) | Angle-Side-Angle (ASA) | B) | Angle-Angle-Side
(AAS) | D) | Side-Side-Side (SSS) |
|
|
|
15.
|
Given the measures shown in the diagram, which two triangles are
congruent? A) | D and R | B) | G and W | C) | G and R | D) | D and
W |
|
|
|
16.
|
Given: 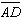 and and 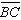 intersect
at X intersect
at X
AX = XB
CX = XD
Which congruency
statement is true? | 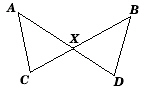 | | |
|
|
|
17.
|
Which triangle below is not congruent to the other three
triangles?
|
|
|
18.
|
Given: Angle DAC congruent to angle
CBD and
Angle ADC congruent to angle BCD
Which could be used to prove 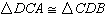 ? ? | 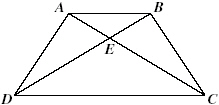 | | |
A) | (AAS) If 2 angles and a side not between them in one triangle are congruent to
2 angles and a side not between them in another triangle, then the triangles are
congruent | B) | (SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle,
then the triangles are congruent | C) | (SAS) If 2 sides and the angle between
them in one triangle are congruent to 2 sides and the angle between them in another triangle, then
the triangles are congruent | D) | (ASA) If 2 angles and the side between
them in one triangle are congruent to 2 angles and the side between them in another triangle, then
the triangles are congruent |
|
|
|
19.
|
The figure has angle measures as shown.
What is the measure of 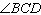 ? ? |  | | |
|
|
|
20.
|
Given: Segment BD bisects AE at
C and
Angle BAC congruent to angle DEC
Which could be used to prove 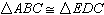 ? ? | 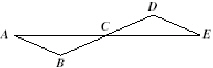 | | |
A) | (ASA) If 2 angles and the side between them in one triangle are congruent to 2
angles and the side between them in another triangle, then the triangles are
congruent | B) | (AAS) If 2 angles and a side not between them in one triangle are congruent to
2 angles and a side not between them in another triangle, then the triangles are
congruent | C) | (SAS) If 2 sides and the angle between them in one triangle are congruent to 2
sides and the angle between them in another triangle, then the triangles are
congruent | D) | (SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle,
then the triangles are congruent. |
|
|
|
21.
|
Sam finished proving that  .
Using Sam’s diagram to the right,
which is a pair of corresponding angles? | 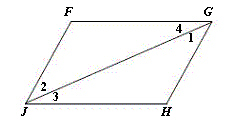 | | |
|
|
|
22.
|
What value of x makes  ? 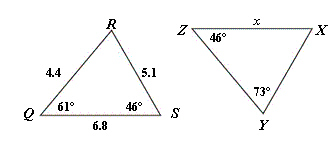 A) | x = 9.5 | B) | x = 6.8 | C) | x = 5.1 | D) | x =
4.4 |
|
|
|
23.
|
|
|
|
24.
|
Triangles FXV, FTV, and JXV are show on the coordinate grid, and all the vertices have
coordinates that are
integers.
Which
statement is true? | 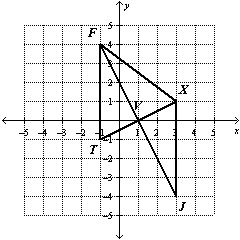 | | |
A) | No two triangles are congruent. | B) | Only  and and  are
congruent. are
congruent. | C) | Only 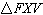 and and 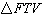 are congruent. are congruent. | D) | Triangle FXV,
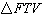 , and , and 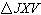 are all congruent are all congruent |
|
|
|
25.
|
A) | (0, 3) | B) | (0, 4) | C) | (1, 4) | D) | (1,
3) |
|