Name:     ID: 
 
Email: 

Cumulative Ch 5 Gateway

 1. 
A trapezoid is located entirely in quadrant III. If this trapezoid is reflected across the origin, in which quadrant will the new trapezoid be located?
A)
I
B)
III
C)
IV
D)
II
 

 2. 
Which is the contrapositive of the statement below?
  If you do your homework, then you will be prepared for the test.
A)
If you are not prepared for the test, then you did not do your homework.
B)
If you do your homework, then you will be prepared for the test.
C)
If you are prepared for the test, then you did your homework.
D)
If you did not do your homework, then you will not be prepared for the test.
 

 3. 
Given:
Segment AC congruent to segment AB  and
Segment DC congruent to segment DB


             
Which could be used to prove 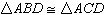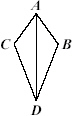mc003-1.jpg?		mc003-2.jpg
 
A)
(SAS) If 2 sides and the angle between them in one triangle are congruent to 2 sides and the angle between them in another triangle, then the triangles are congruent
B)
(SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle, then the triangles are congruent
C)
(AAS) If 2 angles and a side not between them in one triangle are congruent to 2 angles and a side not between them in another triangle, then the triangles are congruent
D)
(ASA) If 2 angles and the side between them in one triangle are congruent to 2 angles and the side between them in another triangle, then the triangles are congruent
 

 4. 
What value of x makes 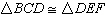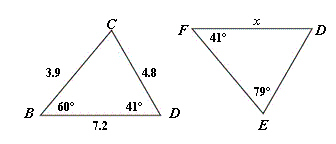mc004-1.jpg?
mc004-2.jpg
A)
x = 4.8
B)
x = 7.2
C)
x = 3.9
D)
x = 8.7
 

 5. 
With the information given in the drawings, which pair of triangles can be proven congruent by the Angle-Angle-Side theorem?
A)
mc005-2.jpg
C)
mc005-4.jpg
B)
mc005-3.jpg
D)
mc005-5.jpg
 

 6. 
In the figure shown,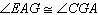
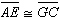mc006-1.jpg and mc006-2.jpg.





Which of the following must be true?		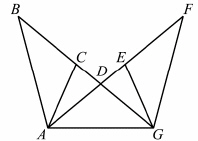mc006-3.jpg
A)
mc006-4.jpg
C)
mc006-6.jpg
B)
mc006-5.jpg
D)
mc006-7.jpg
 

 7. 
In the figure below, 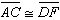mc007-1.jpg and 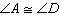 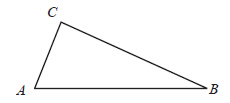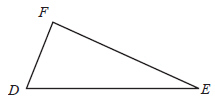mc007-2.jpg.
mc007-3.jpgmc007-4.jpg
Which additional information would be enough to prove that 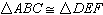mc007-5.jpg?
A)
mc007-6.jpg
B)
mc007-7.jpg
C)
mc007-8.jpg
D)
mc007-9.jpg
 

 8. 
Which triangle below is not congruent to the other three triangles?
A)
mc008-1.jpg
C)
mc008-3.jpg
B)
mc008-2.jpg
D)
mc008-4.jpg
 

 9. 
Given:
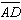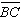mc009-1.jpg and mc009-2.jpg intersect at X
AX = XB
CX = XD

Which congruency statement is true?		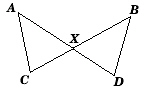mc009-3.jpg
A)
mc009-6.jpg
B)
mc009-7.jpg
C)
mc009-8.jpg
D)
mc009-9.jpg
 

 10. 
How many different lines of symmetry does a regular heptagon have?
A)
1
B)
7
C)
6
D)
5
 

 11. 
Given:
Angle DAC congruent to angle CBD  and
Angle ADC congruent to angle BCD


             
Which could be used to prove 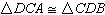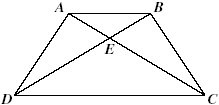mc011-1.jpg?		mc011-2.jpg
 
A)
(SAS) If 2 sides and the angle between them in one triangle are congruent to 2 sides and the angle between them in another triangle, then the triangles are congruent
B)
(ASA) If 2 angles and the side between them in one triangle are congruent to 2 angles and the side between them in another triangle, then the triangles are congruent
C)
(SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle, then the triangles are congruent
D)
(AAS) If 2 angles and a side not between them in one triangle are congruent to 2 angles and a side not between them in another triangle, then the triangles are congruent
 

 12. 
The figure has angle measures as shown.

                          




             
What is the measure of ÐBCD?		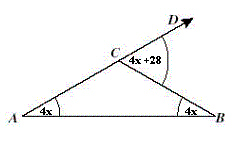mc012-1.jpg
A)
56°
B)
28°
C)
76°
D)
124°
 

 13. 
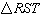mc013-1.jpg and 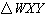mc013-2.jpg are congruent.





What is the measure of 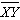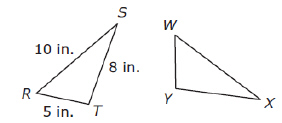mc013-3.jpg?		mc013-4.jpg
A)
8 in
B)
5 in
C)
10 in
D)
9 in
 

 14. 
DL'M'N' is apparently the result of:
mc014-1.jpg
A)
rotating DLMN about the point (–3, 4)
C)
reflecting DLMN across the line y=x
B)
reflecting DLMN across the x-axis
D)
reflecting DLMN across the y-axis
 

 15. 
The slope of the line joining the coordinate points  (7, –4) and (2, 3) is
A)
mc015-3.jpg
B)
mc015-4.jpg
C)
mc015-5.jpg
D)
mc015-6.jpg
 

 16. 
Given:
Segments AE and BD bisect each other at C 

             
Which could be used to prove 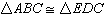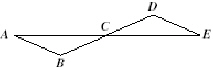mc016-1.jpg?		mc016-2.jpg
 
A)
(ASA) If 2 angles and the side between them in one triangle are congruent to 2 angles and the side between them in another triangle, then the triangles are congruent
B)
(AAS) If 2 angles and a side not between them in one triangle are congruent to 2 angles and a side not between them in another triangle, then the triangles are congruent
C)
(SAS) If 2 sides and the angle between them in one triangle are congruent to 2 sides and the angle between them in another triangle, then the triangles are congruent
D)
(SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle, then the triangles are congruent.
 

 17. 
If 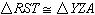mc017-1.jpg, which statement is always true?
A)
mc017-4.jpg
B)
mc017-5.jpg
C)
mc017-6.jpg
D)
mc017-7.jpg
 

 18. 
Given:
M is the midpoint of segment KP  and
Angle KLM congruent to angle MNP


 

           
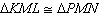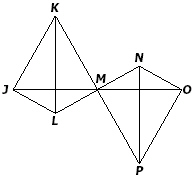The given information is sufficient to prove mc018-1.jpg by which postulate/theorem?		mc018-2.jpg
 
A)
Angle-Side-Angle
C)
Side-Angle-Side
B)
Side-Side-Side
D)
Angle-Angle-Side
 

 19. 
Which set of information
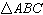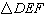is NOT enough to prove that mc019-1.jpg is congruent to mc019-2.jpg ?
mc019-3.jpg
A)
mc019-4.jpg
B)
mc019-5.jpg
C)
mc019-6.jpg
D)
mc019-7.jpg
 

 20. 
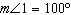
Given: mc020-1.jpg






Which must be true if y || z?		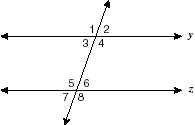mc020-2.jpg
A)
mc020-4.jpg
B)
mc020-5.jpg
C)
mc020-6.jpg
D)
mc020-7.jpg
 

 21. 
Use the proof to answer the question below:
Given:  mc021-1.jpg
           mc021-2.jpg

Prove:  mc021-3.jpg		mc021-4.jpg
Statement
Reason
mc021-5.jpgGiven
mc021-6.jpgmc021-7.jpg
mc021-8.jpgReflexive Property of Congruence
mc021-9.jpg???

What reason can be used to prove that the triangles are congruent?
A)
ASA
B)
SSS
C)
SAS
D)
AAS
 

 22. 
The distance between the points (–6, 9) and (2, –7) is:
A)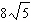
mc022-3.jpg
B)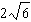
mc022-4.jpg
C)
320
D)
24
 

 23. 
mc023-1.jpg
What is the measure of mc023-2.jpg?mc023-3.jpg
A)
98°
B)
74°
C)
57°
D)
25°
 

 24. 
Given:
E is a midpoint of AC
Angle DAE congruent to angle BCE



Based on the information given, 	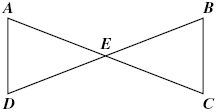	mc024-1.jpg
which triangle congruence theorem could be used to prove 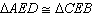mc024-2.jpg?
A)
Angle-Angle-Side (AAS)
C)
Side-Side-Side (SSS)
B)
Side-Angle-Side (SAS)
D)
Angle-Side-Angle (ASA)
 

 25. 
Given:
Segment AD congruent to segment AC  and
Angle DBA congruent to angle CEA


             
Which could be used to prove 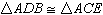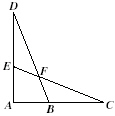mc025-1.jpg?		mc025-2.jpg
 
A)
(SSS) If 3 sides of one triangle are congruent to 3 sides of another triangle, then the triangles are congruent.
B)
(SAS) If 2 angles and a side not between them in one triangle are congruent to 2 angles and a side not between them in another triangle, then the triangles are congruent
C)
(ASA) If 2 angles and the side between them in one triangle are congruent to 2 angles and the side between them in another triangle, then the triangles are congruent
D)
(AAS) If 2 angles and the side between them in one triangle are congruent to 2 angles and the side between them in another triangle, then the triangles are congruent
 



 
         Start Over