Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
The measure of the angle 330 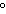 in standard position
is given. Find two positive angles and two negative angles that are coterminal with the given
angle. a. | 426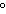 , 786 , 786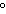 ,
–294 ,
–294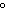 , –654 , –654 | c. | 710 , 1020 , 1020 ,
–50 ,
–50 , –360 , –360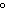 | b. | 670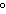 ,
1060 ,
1060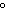 , –70 , –70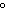 , –345 , –345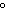 | d. | 690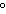 ,
1050 ,
1050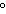 , –30 , –30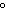 , –390 , –390 |
|
|
|
2.
|
The measure of the angle 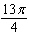 in standard position is
given. Find minimal positive angle and maximal negative angles that are coterminal with the given
angle.
|
|
|
3.
|
What is the side labeled x equal to, if y = 22? 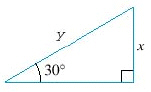
|
|
|
4.
|
A 109 ft tree casts a shadow that is 130 ft long. What is the angle of elevation
of the sun?
|
|
|
5.
|
Find the reference angle for the angle measuring 921 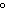 .
|
|
|
6.
|
Find the reference angle for the angle measuring 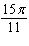 .
|
|
|
7.
|
Write the following trigonometric expression in terms of sine and cosine, and
then simplify.
cos x tan x
|
|
|
8.
|
Simplify the following trigonometric expression.
tan x cos
x csc x
a. | sin x | b. | 1 | c. | cot x | d. | sin 2
x |
|
|
|
9.
|
Find the exact value of the expression. 
|
|
|
10.
|
Find the exact value of the expression. 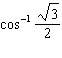
|
|
|
11.
|
Find the exact value of the expression. 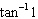
|
|
|
12.
|
For the function f whose graph is given, state the value of the given
quantity, if it exists. 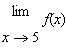 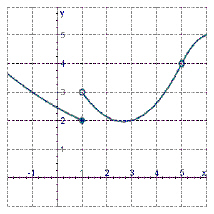 a. | 3 | b. | Does not exist. | c. | 4 | d. | 5 | e. | 2 |
|
|
|
13.
|
Find the exact value of the expression. 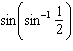
|
|
|
14.
|
Find the exact value of the expression. 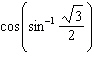
|
|
|
15.
|
Evaluate the expression by sketching a triangle. 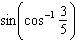
|
|
|
16.
|
Evaluate the limit: 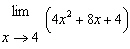 .
|
|
|
17.
|
Evaluate the limit: 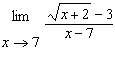 . a. | 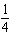 | b. | 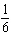 | c. | 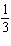 | d. | The limit does not
exist. |
|
|
|
18.
|
Find the slope of the tangent line to the graph of f at the point ( 1, 0
).
f ( x ) = 3 + 5x – 8x 2
|
|
|
19.
|
Find an equation of the tangent line to the curve at x = -3. 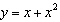 a. | y = –5x – 9 | c. | y = –4x –
27 | b. | y = 5x – 27 | d. | y = –4x +
9 |
|
|
|
20.
|
Sketch the graph of the piecewise defined function. 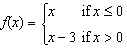
|
|
|
21.
|
The graph of a function is sketched below. 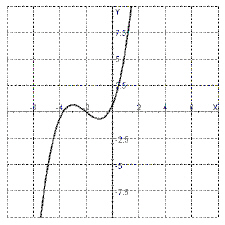 Determine the interval on which the function is decreasing. a. | 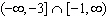 | b. | [1,
3] | c. | [–1, –1] | d. | 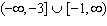 | e. | [–3,
–1] |
|
|
|
22.
|
The graph shows the depth of water W in a reservoir over a one-year
period, as a function of the number of days x since the beginning of the year. What was the
average rate of change in W between x = 100 and x = 200? 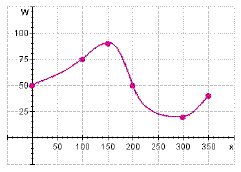 a. | –0.35 | b. | –0.245 | c. | –0.2 | d. | –0.26 | e. | –0.25 |
|
|
|
23.
|
Find the x- and y-intercepts of the rational function 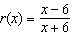 . a. | x-intercept (6, 0), y-intercept (0, –1) | b. | x-intercept
(6, 0), y-intercept (0, –3) | c. | x-intercept (1, 0), y-intercept
(0, 6) | d. | x-intercept (–1, 0), y-intercept (0, 6) | e. | x-intercept
(–6, 0), y-intercept (0, 0) |
|
|
|
24.
|
Find the horizontal and vertical asymptotes of the rational function 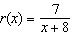 . a. | horizontal asymptote y = 7; vertical asymptote x =
8 | b. | horizontal asymptote y = 7; vertical asymptote x =
–8 | c. | horizontal asymptote y = 0; vertical asymptote x =
–16 | d. | horizontal asymptote y = 0; vertical asymptote x =
–8 | e. | horizontal asymptote y = 0; vertical asymptote x =
8 |
|
|
|
25.
|
The rabbit population on Mr. Jenkins' farm follows the formula: 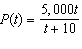 . For this formula, t > 0 is the time in months since the beginning of the year.
What is the eventual population of rabbits? a. | 4500 rabbits | d. | 5500 rabbits | b. | 5750 rabbits | e. | 6000 rabbits | c. | 5000
rabbits |
|
|
|
26.
|
Complete the table of values (to five decimal places) and use the table to
estimate the value of the limit. 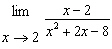 x | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 | f(x) | | | | | | | | | | | | | |
a. | 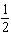 | b. | 6 | c. | The limit does not
exist. | d. | 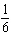 |
|
|
|
27.
|
Complete the table of values (to five decimal places) and use the table to
estimate the value of the limit. 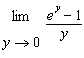 y | –0.1 | –0.01 | –0.001 | 0.001 | 0.01 | 0.1 | f(y) | | | | | | | | | | | | | |
a. | 0 | b. | e | c. | 1 | d. | The limit does not
exist. |
|
|
|
28.
|
Use the following graph and any other graphing device that you need to determine
whether the limit exists. If the limit exists, estimate its value to two decimal places. 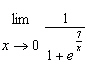 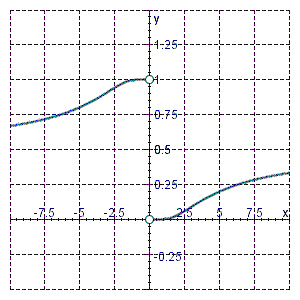 a. | 0.5 | b. | Does not exist. | c. | 1 | d. | 0 |
|
|
|
29.
|
Given that 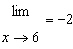 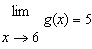 . Evaluate the
limit: 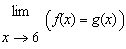 .
|
|
|
30.
|
If an arrow is shot upward on the moon with a velocity of 51 m/s its height (in
meters) after t seconds is given by 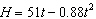 . When will the arrow hit
the moon? Round the result to the nearest thousandth if necessary. a. | 57.845 | b. | 57.956 | c. | 57.944 | d. | 57.955 | e. | 57.96 |
|
|
|
31.
|
A cardiac monitor is used to measure the heart rate of a patient after surgery.
It compiles the number of heartbeats after t minutes. When the data in the table are graphed,
the slope of the tangent line represents the heart rate in beats per minute. Find the average heart
rate (slope of the secant line) over the time interval [ 40, 42 ]. t (min) | 36 | 38 | 40 | 42 | 44 | Heartbeats | 2,536 | 2,664 | 2,808 | 2,940 | 3,070 | | | | | | |
|
Numeric Response
|
|
|
32.
|
Find the exact value of the trigonometric function at the given real
number. 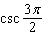
|
|
|
33.
|
Find the exact value of the trigonometric function at the given real
number. 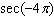
|
|
|
34.
|
Find the limit. 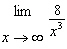
|
|
|
35.
|
A tank contains 4,000 L of pure water. Brine that contains 10 g of salt per
liter of water is pumped into the tank at a rate of 25 L/min. The concentration of salt after
t minutes (in grams per liter) is 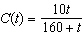 . What happens to the
concentration as 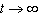 ? __________ g/L
|
Short Answer
|
|
|
36.
|
Find the degree measure of the angle with the given radian
measure. (a) 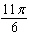 (b) (b)
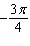 __________  __________ 
|
|
|
37.
|
Find the exact values of the six trigonometric ratios of the angle 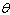 in the triangle.Enter your answer as a fraction.  Find
sec 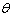
|
|
|
38.
|
Find the reference angle for the given angle. 210 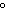
|
|
|
39.
|
Find the reference angle for the given angle. (If needed, type pi for 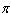 in your answer) 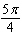
|
|
|
40.
|
Find the exact value for each trigonometric function. cos 150 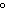
|
|
|
41.
|
Find the exact value for each trigonometric function. sin 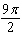
|
|
|
42.
|
Find the value of tan 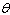 from the information
given. 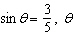 in quadrant II
|
|
|
43.
|
|
|
|
44.
|
Find the limit. 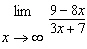
|
|
|
45.
|
Find the limit. 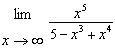
|
|
|
46.
|
A ball is thrown across a playing field. Its path is given by the equation 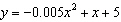 , where x is the distance the ball has traveled horizontally, and y is its
height above ground level, both measured in feet.  How far has it
traveled horizontally when it hits the ground? Please round your answer to the nearest
tenth. __________ ft
|
|
|
47.
|
A manufacturer finds that the revenue generated by selling x units of a
certain commodity is given by the function 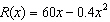 , where the revenue
R(x) is measured in dollars. (a) What is the maximum revenue?
|
|
|
48.
|
The downward velocity of a falling raindrop at time t is modeled by the
function 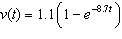 . Find the terminal velocity of the
raindrop by evaluating 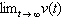 .
|
|
|
49.
|
A jet is flying through a wind that is blowing with a speed of 40 mi/h in the
direction N 35º E. The jet has a speed of 714 mi/h in still air, and the pilot heads the jet in
the direction N 50º E. Find the true speed of the jet.
|
|
|
50.
|
Comments/Concerns
|