|
|
|
1.
|
Find the slope and y-intercept of the line and draw its
graph. 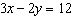
|
|
|
2.
|
Find the slope of the line through P(–9, –3) and Q(–5,
–15).
|
|
|
3.
|
Determine the slope of the line which is sketched below. 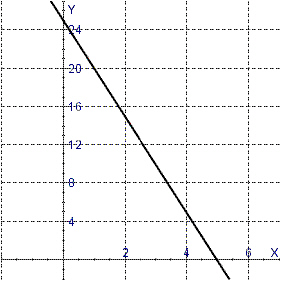 a. | m = –5 | b. | m = 1 | c. | m =
–4 | d. | m = –10 | e. | m =
–2 |
|
|
|
4.
|
Sketch the graph of the function by first making a table of values. 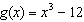
|
|
|
5.
|
Sketch the graph of the piecewise defined function. 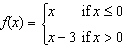
|
|
|
6.
|
Sketch the graph of the piecewise defined function. 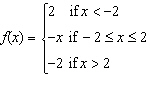
|
|
|
7.
|
What is the domain and range of the function that is graphed below? 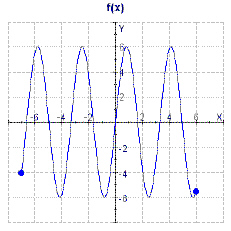 a. | Domain: (–7, 6), Range: [–6, 6] | d. | Domain: [–7, 6],
Range:  | b. | Domain:  , Range: [–6, 6] , Range: [–6, 6] | e. | Domain: [–6, 6], Range: [–7, 6] | c. | Domain:
[–7, 6], Range: [–6, 6] |
|
|
|
8.
|
Determine the interval on which the function in the graph below is
decreasing. 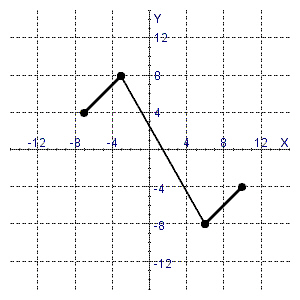 a. | [4, –1] | b. | [–7,
–3] | c. | [–3, 6] | d. | [–2, 7] | e. | [6,
10] |
|
|
|
9.
|
The graph of a function is given as follows: 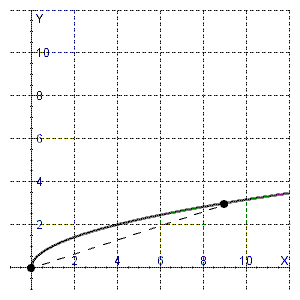 Determine the average rate of change for the function between the indicated values
of the variable.
|
|
|
10.
|
What is the average rate of change of the function 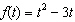 between 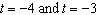 ?
|
|
|
11.
|
The graph of the function y = – x 2 + 4 x
is: 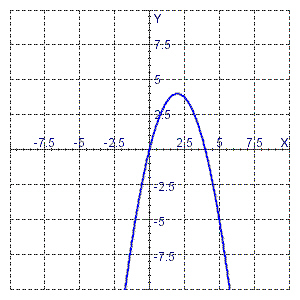 Find the coordinates of its vertex and
its intercepts.
|
|
|
12.
|
The graph of the function y = x 2 – 6 x + 8
is: 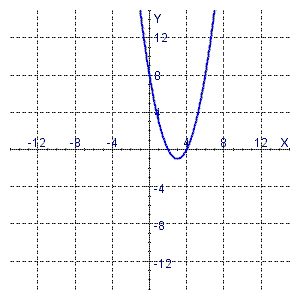 Find the coordinates of its vertex and
its intercepts.
|
|
|
13.
|
Find the maximum or minimum value of the function. 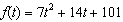
|
|
|
14.
|
The graph of a quadratic function 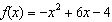 is
given. (a) Find the coordinates of the vertex. (__________,
__________) (b) Find the maximum or minimum value of f.
|
|
|
15.
|
Solve the system, or show that it has no solution. If the system has infinitely
many solutions, express them in the ordered-pair form. 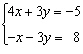 a. | The system has no solution. | b. | x = 1, y = 3 | c. | x = 0,
y = –4 | d. | 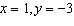 | e. | The system has
infinitely many solutions. 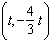 |
|
|
|
16.
|
Solve the system. 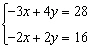
|
|
|
17.
|
Solve the system, or show that it has no solution. If the system has infinitely
many solutions, express them in the ordered-pair form. 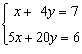
|
|
|
18.
|
Calculator Allowed: Solve the
System 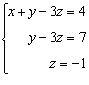
|
|
|
19.
|
Calculator Allowed: Find the complete
solution of the linear system: 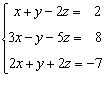
|
|
|
20.
|
Calculator Allowed: In a suspension
bridge the shape of the suspension cables is parabolic. The bridge shown in the figure has towers
that are 800 m apart, and the lowest point of the suspension cables is 200 m below the top of the
towers. Find the equation of the parabolic part of the cables, placing the origin of the coordinate
system at the vertex. NOTE: This equation is used to find the length of cable needed in the
construction of the bridge. 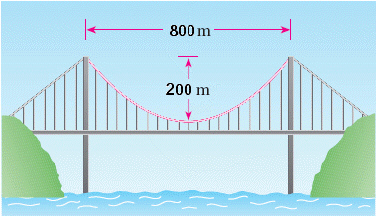
|
|
|
21.
|
Find the vertices of the ellipse. 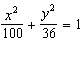 a. | (–6, 0) and (6, 0) | b. | none of these | c. | (–1, 0) and
(1, 0) | d. | (–8, 0) and (8, 0) | e. | (–10, 0) and (10,
0) |
|
|
|
22.
|
Calculator Allowed: A
"sunburst" window above a doorway is constructed in the shape of the top half of an
ellipse, as shown in the figure. The window is 15 in. tall at its highest point and 60 in. wide at
the bottom. Find the height of the window 25 in. from the center of the base. 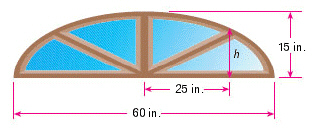 Please round your answer to the nearest tenth. __________ in.
|
|
|
23.
|
Find the vertices of the hyperbola. 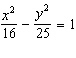
|
|
|
Simplify the expression. Write your answer using only positive
exponents.
|
|
|
24.
|
|
|
|
25.
|
|
|
|
26.
|
|
|
|
Solve the equation.
|
|
|
27.
|
|
|
|
28.
|
|
|
|
Factor the polynomial completely.
|
|
|
29.
|
|
|
|
30.
|
The graph of 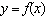 is shown. Use the graph to identify the
factors of 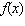 . 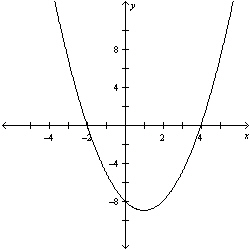
|
|
|
31.
|
Write a linear function f with the values 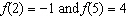 .
|
|
|
Evaluate the expression.
|
|
|
32.
|
a. | 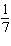 | b. | 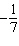 | c. | 7 | d. | –7 |
|
|
|
33.
|
a. | 5 | c. | not a real number | b. | –375 | d. | –5 |
|
|
|
34.
|
|
|
|
35.
|
Which expression is different?
|
|
|
36.
|
Which is a factor of the trinomial 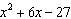 ?
|
|
|
37.
|
Does 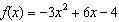 have a maximum or minimum? Find the
value. a. | maximum; 1 | b. | minimum; 1 | c. | maximum; 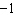 | d. | minimum; 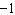 |
|
|
|
Choose the quadratic function in standard form whose graph satisfies the
given condition(s).
|
|
|
38.
|
x-intercepts: –1 and –5
|
|
|
39.
|
|