| A | B |
|---|
| Through any two points, there is EXACTLY ONE line. | 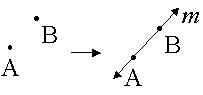 |
| A line contains AT LEAST 2 points. | 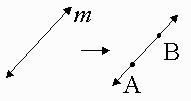 |
| Through any 3 noncollinear points, there is EXACTLY ONE plane. | 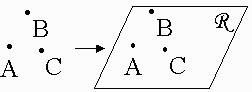 |
| A plane contains at least 3 NONCOLLINEAR points. | 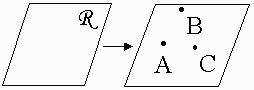 |
| If 2 points lie in a plane, then the ENTIRE line containing those 2 points lies in that plane. | 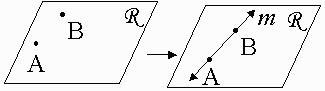 |
| If 2 planes intersect, then their intesection is a line. | 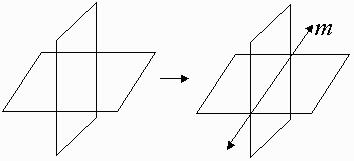 |
| If 2 lines intersect, then they intersect at EXACTLY ONE point. | 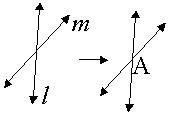 |
| If B is between A and C, then AB + BC = AC. |  |
| If C is in the interior of angle BAD, then the measure of angle BAD=the measure of angle BAC+CAD. |  |
| Reflexive Property of Segment Congruence | For any segment AB, segment AB is congruent to segment AB |
| Symmetric Property of Segment Congruence | If segment AB is congruent to segment CD, then segment CD is congruent to segment AB |
| Transitive Property of Segment Congruence | If segment AB is congruent to segment CD, and segment CD is congruent to segment EF, then segment AB is congruent to segment EF |
| Reflexive Property of Angle Congruence | For any angle A, angle A is congruent to angle A |
| Symmetric Property of Angle Congruence | If angle A is congruent to angle B, then angle B is congruent to angle A |
| Transitive Property of Angle Congruence | If angle A is congruent to angle B and angle B is congruent to angle C, then angle A is congruent to angle C |
| Right Angle Congruence Theorem | All right angles are congruent |
| Congruent Supplements Theorem-If two angles are supplementary to the same angle (or to congruent angles) then they are congruent | add image for this question |
| Congruent Complements Theorem-If two angles are complementary to the same angle (or to congruent angles) then the two angles are congruent | add image for this question |
| Linear Pair Postulate-If two angles form a linear pair, then they are supplementary | add image for this question |
| Vertical Angles Theorem-Vertical angles are congruent | add image for this question |
| Addition Property of Equality | If a = b, then a + c = b + c |
| Subtraction Property of Equality | If a = b, then a - c = b - c |
| Multiplication Property of Equality | If a = b, then ac = bc |
| Division Property of Equality | If a = b and c does not equal 0, then a divided by c = b divided by c |
| Reflexive Property of Equality | For any real number a, a = a |
| Symmetric Property of Equality | If a = b, then b = a |
| Tansitive Property of Equality | If a = b and = c, then a = c |
| Substitution Property of Equality | If a = b, then a can be substituted for b in any equation or expression |