| A | B |
|---|
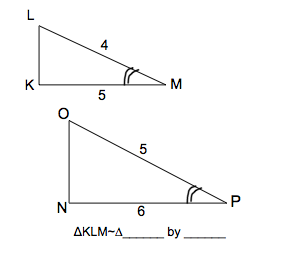 | Not similar. The smaller triangle has a 4:5 ratio in the sides, the larger has a 5:6 |
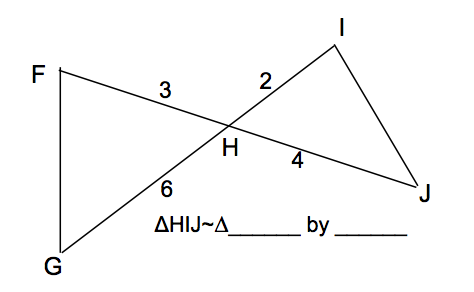 | HFG by SAS. I is congruent to F in this configuration. |
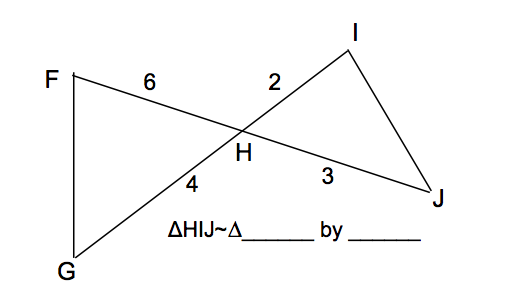 | HGF by SAS. I is congruent to G in this configuration. |
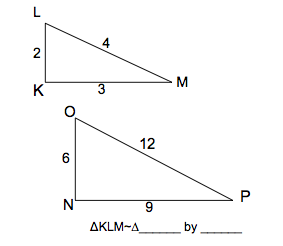 | NOP by SSS. All three sides of the larger triangle are 3 times the size of the smaller. |
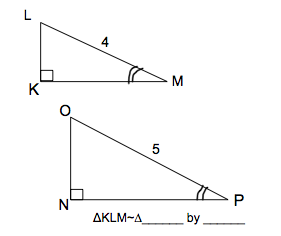 | NOP by AA |
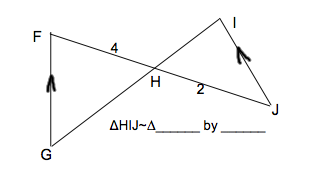 | HGF by AA. The given side lengths only tell us the larger triangle is twice the size of the smaller. |
 | Not necessarily similar. All we have is that the smaller triangle is isosceles. |
 | DBE by SAS. The larger triangle is twice the size of the smaller, and shares a vertex. |
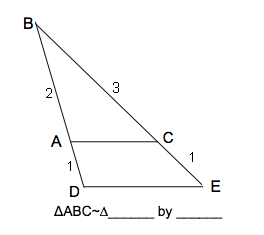 | Not similar. The smaller triangle has a 2:3 ratio of sides, the larger a 3:4. |
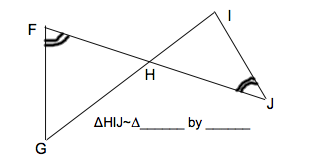 | HGF by AA |
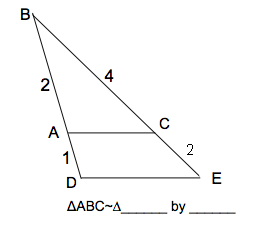
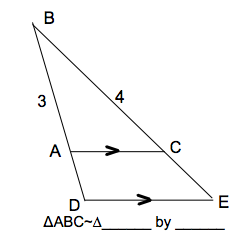 | DBE by AA. We do not have information on the lengths of the larger triangle, so we cannot use SAS. |
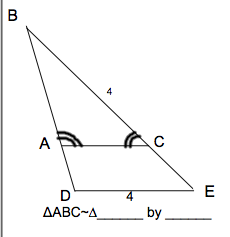
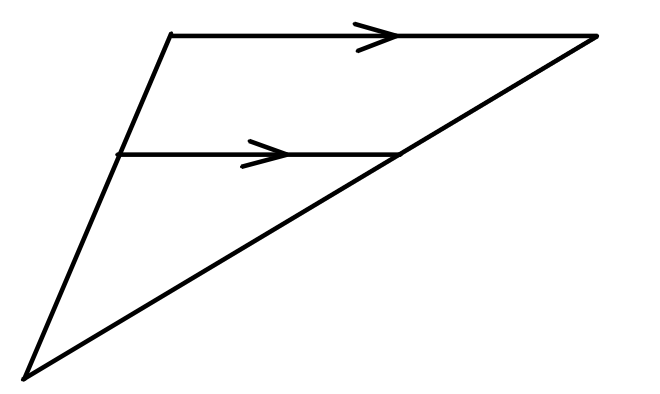 | Similar by AA. The two triangles share an angle, and the parallel lines create a pair of congruent corresponding angles. |
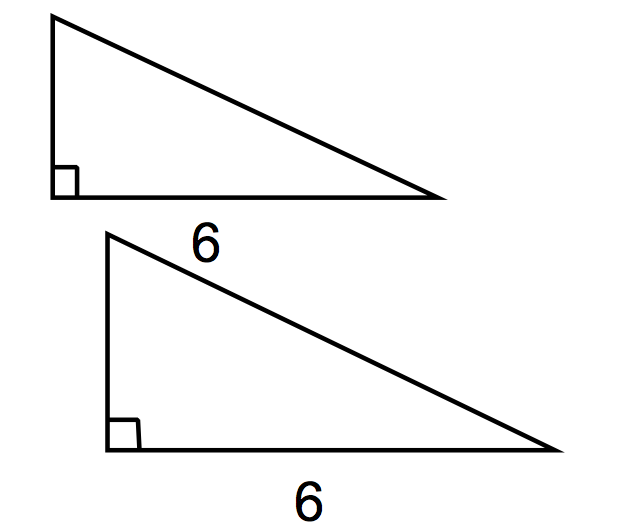 | Not necessarily congruent or similar. Only 2 elements in each triangle are known (one angle and one side). 3 are required to determine similarity or congruence. |
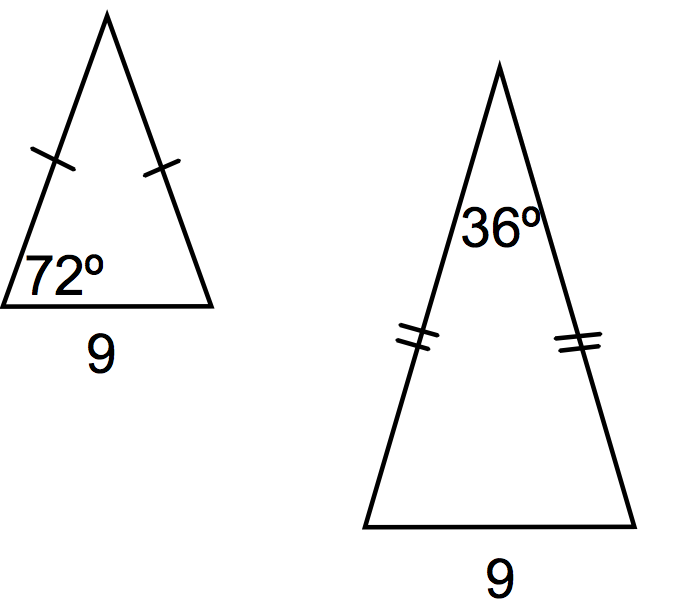 | ASA congruence. We can easily determine the angles are congruent, and one side is congruent. |
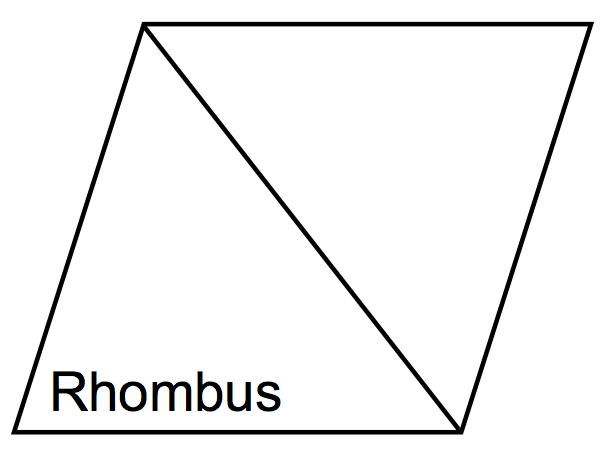 | SSS congruence. The sides of a rhombus are congruent, and the shared side is congruent to itself. |
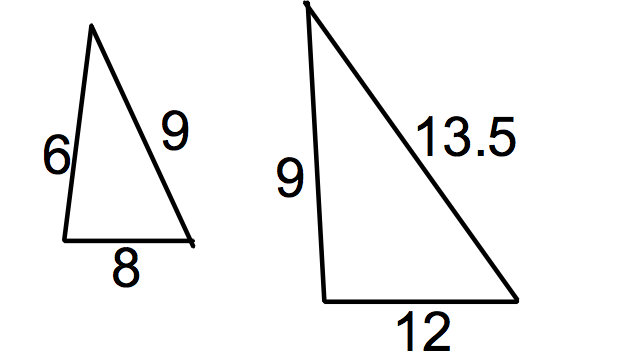 | SSS similarity. All 3 sides of the larger triangle are in the ratio 3:2 when compared to the smaller triangle. |