1.2.3 Análisis de circuitos RLC

Método de la Substitución

El método de la substitución es generalmente utilizado en el análisis de circuitos de reducida complejidad. Dos ejemplos de circuitos de este tipo son las redes representadas en la figura

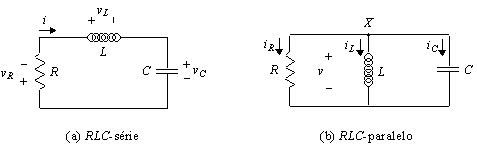
Considérese entonces el circuito RLC en serie sin fuentes independientes representado en la figura a). La aplicación de la Ley de Kirchhoff de los voltajes a malla única del circuito permite escribir la igualdad

al cual, en conjunto con las características voltaje-corriente de los componentes, se puede re-escribir como

en que i(t) y vC(t) definen, respectivamente, la corriente en la bobina (y en el capacitor) y el voltaje en el capacitor. Por lo tanto, por substitución de la característica voltaje-corriente del capacitor, i(t)=CdvC(t)/dt, se obtiene

o, dividiendo entre LC,

En el caso de que el objetivo del análisis consistiese en la determinación de la ecuación diferencial que gobierna la corriente en la bobina, iL(t), entonces el paso entre las ecuaciones debería haber sido efectuada recurriendo ala característica inversa del capacitor,

esto es, a través de la escrita en la forma (iL=iC=i)

En este caso, la aplicación del operador derivada a las partes izquierda y derecha de la igualdad

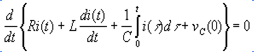
conduce a la ecuación diferencial de 2do orden          

cuya forma es idéntica a aquella establecida anteriormente para el voltaje en las terminales del capacitor.

De acuerdo con el ejemplo anterior, pueden identificarse en este método los siguientes pasos:

(i) obtención de una ecuación que contienen las variables relativas en los dos elementos almacenadores de energía, propiamente el voltaje en las terminales del capacitor y la corriente en la bobina;

(ii) substitución de la variable en él deseada, en este caso recurriendo a las características voltaje-corriente del capacitor o de la bobina;

(iii) cuando sea necesario, derivación de ambos los términos de la ecuación diferencial a modo de obtener una ecuación diferencial de 2do orden.

Considérese ahora el circuito RLC en paralelo representado en la figura b) y admítase que se pretende determinar la ecuación diferencial que gobierna el voltaje en las terminales del capacitor, vC(t). La aplicación de la Ley de Kirchhoff de las corrientes al nodo X permite escribir la igualdad

o sea,

en este caso, la substitución de la característica voltaje-corriente de la bobina

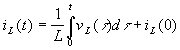
permite re-escribirlo en la forma

que, después por derivación, conduce a la ecuación diferencial de 2do orden